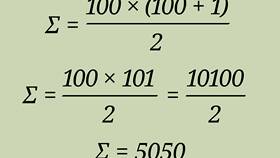Нахождение суммы членов последовательности или множества - распространенная математическая задача, применяемая в различных областях вычислений. Рассмотрим основные методы расчета суммы элементов.
Содержание
Основные понятия
| Термин | Определение |
| Член последовательности | Отдельный элемент числового ряда |
| Сумма членов | Результат сложения всех элементов множества |
| Конечная последовательность | Ряд с ограниченным количеством элементов |
| Бесконечный ряд | Последовательность с неограниченным числом членов |
Методы нахождения суммы
Арифметическая прогрессия
Для последовательности вида a₁, a₂, a₃, ..., aₙ, где aₙ = a₁ + d(n-1):
- Формула суммы: Sₙ = n/2 × (a₁ + aₙ)
- Альтернативная форма: Sₙ = n/2 × [2a₁ + d(n-1)]
- Где d - разность прогрессии, n - количество членов
Геометрическая прогрессия
Для последовательности вида b₁, b₂, b₃, ..., bₙ, где bₙ = b₁ × rⁿ⁻¹:
- Конечная сумма: Sₙ = b₁(1 - rⁿ)/(1 - r) при r ≠ 1
- Бесконечная сумма: S = b₁/(1 - r) при |r| < 1
- Где r - знаменатель прогрессии
Сумма натуральных чисел
- Сумма первых n натуральных чисел: S = n(n+1)/2
- Сумма квадратов: S = n(n+1)(2n+1)/6
- Сумма кубов: S = [n(n+1)/2]²
Примеры вычислений
| Тип последовательности | Пример | Решение |
| Арифметическая | 2, 5, 8, 11, 14 | S₅ = 5/2 × (2 + 14) = 40 |
| Геометрическая | 3, 6, 12, 24 | S₄ = 3(1-2⁴)/(1-2) = 45 |
| Натуральные числа | 1+2+3+...+10 | S = 10×11/2 = 55 |
Программная реализация
- Использование цикла for для итеративного сложения
- Рекурсивные функции для последовательностей
- Библиотечные функции (например, sum() в Python)
- Векторизованные вычисления в NumPy
Практические рекомендации
- Для больших n используйте аналитические формулы вместо перебора
- Проверяйте сходимость бесконечных рядов перед вычислением
- Учитывайте погрешности округления при работе с вещественными числами
- Для знакопеременных рядов применяйте соответствующие методы